En
matemáticas, una
función,
[1] aplicación o
mapeo f es una
relación entre un conjunto dado
X (el
dominio) y otro conjunto de elementos
Y (el
codominio) de forma que a cada elemento
x del dominio le
corresponde un único elemento del codominio
f(x). Se denota por:

Comúnmente, el término
función se utiliza cuando el codominio son valores numéricos,
reales o
complejos. Entonces se habla de
función real o
función compleja mientras que a las funciones entre conjuntos cualesquiera se las denomina
aplicaci de las funciones.
- Condición de existencia: Todos los elementos de X están relacionados con elementos de Y, es decir,
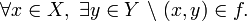
- Condición de unicidad: Cada elemento de X está relacionado con un único elemento de Y, es decir, si

|
Notación y nomenclatura
Al dominio también se le llama
conjunto de entrada o
conjunto inicial. Se denota por

o

. A los elementos del dominio se les llama habitualmente
argumentoone
- La función definida por
 , tiene como dominio, codominio e imagen a todos los números reales
, tiene como dominio, codominio e imagen a todos los números reales 

Función con Dominio X y Rango Y
- Para la función
 tal que
tal que  , en cambio, si bien su dominio y codominio son iguales a
, en cambio, si bien su dominio y codominio son iguales a  , sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
, sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
- En la figura se puede apreciar una función
 , con
, con

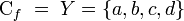
- Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,

- Esta función representada como relación, queda:

Igualdad de funciones
Sean las funciones
f: A → B y
g: C → D, decimos que
f es igual a g y escribimos
f=g si y sólo si se cumple que ambas funciones:
- tienen igual dominio, A=C,
- tienen igual codomino, B=D, y
- tiene la misma asignación, es decir que para cada x se cumple que f(x)=g(x).
Representación de funciones
Las funciones se pueden presentar de distintas maneras:
- usando una relación matemática descrita mediante una expresión matemática: ecuaciones de la forma y = f(x). Cuando la relación es funcional, es decir satisface la segunda condición de la definición de función, se puede definir una función que se dice definida por la relación, A menos que se indique lo contrario, se supone en tales casos que el dominio es el mayor posible (respecto a inclusión) y que el codominio son todos los Reales. El dominio seleccionado se llama dominio natural.
 o
o  . A los elementos del dominio se les llama habitualmente argumentoone
. A los elementos del dominio se les llama habitualmente argumentoone , tiene como dominio, codominio e imagen a todos los números reales
, tiene como dominio, codominio e imagen a todos los números reales 
 tal que
tal que  , en cambio, si bien su dominio y codominio son iguales a
, en cambio, si bien su dominio y codominio son iguales a  , sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
, sólo tendrá como imagen los valores comprendidos entre 0 y +∞. , con
, con
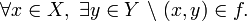



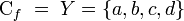

No hay comentarios:
Publicar un comentario